树形结构是一种分层的非线性结构数据, 对于前端来说, 最常见的 DOM 树就是一个典型的树形结构数据
二叉树
二叉树(Binary Tree) 是一种非线性数据结构,代表着祖先与后代之间的派生关系,
体现着“一分为二”的分治逻辑。与链表类似,二叉树的基本单元是节点,每个节点包含一个唯一的 key 和两个指针(一般是left和right)
二叉树的一些概念
- 根节点: 位于二叉树顶层的节点(开始节点, 没有父节点)
- 叶节点: 最底端的节点(没有子节点)
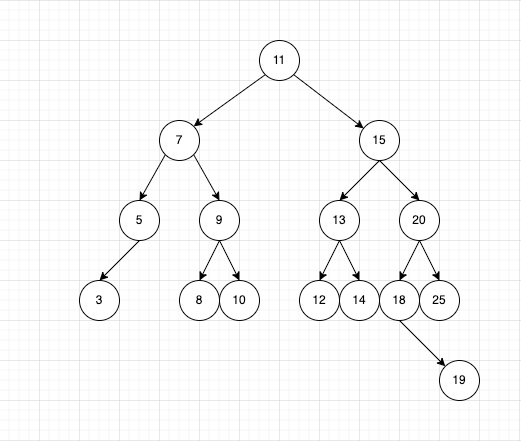
- 子树: 以当前节点为参照物(rootNode), 如图: 15 的左子树(就是 13,12,14), 右子树(就是 20,18,25,11)

二叉树的遍历
- 层序遍历(广度优先)

- 前序/中序/后序遍历(深度优先)

二叉搜索树
二叉搜索树(binary search tree 简称 BST) 也叫 二叉排序树(binary sort tree)
二叉搜索树的特点: 以当前节点为参照物, 左节点的 key 一定比当前节点 key 小, 右节点的 key 一定比当前节点的 key 大
二叉搜索树中的一些概念:
- 前驱节点: 当前节点左子树 key 最大的节点(如图: 7 的前驱就是 5)
- 后继节点: 当前节点右子树 key 最小的节点(如图: 7 的后继就是 8)
实现
接口
typescript
interface TreeNode<T> {
key: number;
value: T;
left: TreeNode | null;
right: TreeNode | null;
}
interface BinarySearchTreeInterface<T> {
rootNode: TreeNode<T> | null;
createTreeNode(key: number, value: T): TreeNode<T>;
keys(): Array<number>;
values(): Array<T>;
hasKey(key: number): boolean;
hasValue(value: T): boolean;
insert(): void;
forEach(handler: (item: TreeNode<T>) => void | false): void;
traversePreOrder(handler: (item: TreeNode<T>) => void): void;
traverseInOrder(handler: (item: TreeNode<T>) => void): void;
traversePostOrder(handler: (item: TreeNode<T>) => void): void;
findMin(): TreeNode<T>;
findMax(): TreeNode<T>;
find: (key: number) => boolean;
remove: (key: number) => boolean;
}具体实现
typescript
/**
* 二叉搜索树
*/
export default class BinarySearchTree<T> {
public rootNode: TreeNode<T> | null = null
/**
* 获取所有节点的 key 并返回
* @returns {Array<number>}
*/
public keys(): Array<number> {
const keys: number[] = [];
if (this.rootNode === null) {
return keys;
}
this.forEach(node => {
keys.push(node.key);
});
return keys;
}
/**
* values
*/
public values(): Array<T> {
const values: Array<T> = [];
if (this.rootNode === null) {
return values;
}
this.forEach((item) => {
values.push(item.value);
});
return values;
}
/**
* 是否包含某个 key
* @param {number} key
* @returns {boolean}
*/
public hasKey(key: number): boolean {
return this.keys().includes(key);
}
/**
* 是否包含某个 value
* @param {T} value
* @returns {boolean}
*/
public hasValue(value: T): boolean {
return this.values().includes(value);
}
/**
* 创建树节点
* @param {number} key
* @param {T} value
* @returns {TreeNode<T>}
*/
public createTreeNode(key: number, value: T): TreeNode<T> {
return {
key,
value,
left: null,
right: null,
};
}
/**
* 插入节点到数中
* @param {number} key
* @param {T} value
*/
public insert(key: number, value: T): void {
if (this.hasKey(key)) {
throw new Error(`[insert]key '${key}' is reduplicated`);
}
const node = this.createTreeNode(key, value);
if (this.rootNode) {
this.insertNode(this.rootNode, node);
} else {
this.rootNode = node;
}
}
/**
* 插入节点的具体操作
* @param node
* @param newNode
*/
private insertNode(node: TreeNode<T>, newNode: TreeNode<T>): void {
const key: "left" | "right" = newNode.key < node.key ? "left" : "right";
if (node[key] === null) {
node[key] = newNode;
} else {
this.insertNode(node[key], newNode);
}
}
/**
* 广度优先: 先序遍历树所有节点(推荐,性能最好,而且可以停止遍历)
* @param handler - 遍历传入的处理函数
*/
public forEach(handler: (node: TreeNode<T>) => void | false) {
const stack: Array<TreeNode<T>> = [this.rootNode!];
while (stack.length) {
const node = stack.shift()!; // 先取左边的节点然后取右边的
node.left && stack.push(node.left);
node.right && stack.push(node.right);
const isContinue = handler(node);
if (isContinue === false) {
break;
}
}
}
/**
* 深度优先(递归): 先序遍历找节点
* @param {'pre'|'in'|'post'} order - 遍历方式
* @param {(node: TreeNode<T>) => void} handler - 遍历处理函数
*/
public traverseNodes(order: 'pre' | 'in' | 'post', handler: (node: TreeNode<T>) => void) {
// 先序遍历: 最先处理当前节点
function traversePreOrder(node: TreeNode<T> | null) {
if (node !== null) {
handler(node);
traversePreOrder(node.left);
traversePreOrder(node.right);
}
}
// 中序遍历: 左边的,然后处理当前节点(节点是升序的)
function traverseInOrder(node: TreeNode<T> | null) {
if (node !== null) {
traverseInOrder(node.left);
handler(node);
traverseInOrder(node.right);
}
}
// 后序遍历: 左边,右边,最后处理当前节点
function traversePostOrder(node: TreeNode<T> | null) {
if (node !== null) {
traversePostOrder(node.left);
traversePostOrder(node.right);
handler(node);
}
}
switch (order) {
case 'pre':
traversePreOrder(this.rootNode);
break;
case 'in':
traverseInOrder(this.rootNode);
break;
case 'post':
traversePostOrder(this.rootNode);
break;
default:
throw new TypeError('[traverseNodes]unknown type');
}
}
/**
* 返回树中的 key 最小的 node
* @returns {TreeNode<T> | null}
*/
public findMin(): TreeNode<T> | null {
let node = this.rootNode!;
if (!node) {
return null;
}
while (node.left) {
node = node.left;
}
return node;
}
/**
* 返回树中的 key 最大的 node
* @returns {TreeNode<T> | null}
*/
public findMax(): TreeNode<T> | null {
let node = this.rootNode!;
if (!node) {
return null;
}
while (node.right) {
node = node.right;
}
return node;
}
/**
* 搜索某个值
* @param {number} key 要搜索的 key
* @returns {null | TreeNode<T>} 返回搜索到的节点或者 null
*/
find(key: number): null | TreeNode<T> {
let target: TreeNode<T> | null = null;
if (this.rootNode === null) {
return target;
}
this.forEach((node) => {
if (node.key === key) {
target = node;
return false;
}
});
return target;
}
/**
* @param {TreeNode<T>} node - 要替换的节点
* @param {boolean} isLeftNode - node 是否是其父节点的 left
* @param {TreeNode<T>} parentNode - node 的父节点
* @param {TreeNode<T> | null} newNode - 新节点
* @returns 返回被替换的接待
*/
private replaceNode(node: TreeNode<T>, isLeftNode: boolean, parentNode: TreeNode<T>, newNode: TreeNode<T> | null) {
if (node === this.rootNode) {
this.rootNode = newNode;
} else if (isLeftNode) {
parentNode.left = newNode;
} else {
parentNode.right = newNode;
}
return node;
}
/**
* 移除传入 key 对应的节点
* @param {number} key
* @returns {TreeNode<T>} 被移除的节点
* @throws {Error} 没有找到要删除的节点就抛出异常
*/
public remove(key: number): TreeNode<T> {
if (this.rootNode === null) {
throw new Error(`[remove]cannot remove '${key}' in empty tree`);
}
let target: TreeNode<T> = this.rootNode!;
let parent: TreeNode<T> = target;
let isLeftNode: boolean = false; // 要删除的节点是其父节点的 left 还是 right
// 先找到要删除的节点, 及其父节点
while (target.key !== key) {
parent = target;
if (key < target.key) {
// 向左查找
target = target.left;
isLeftNode = true;
} else {
// 向右查找
target = target.right;
isLeftNode = false;
}
// 没有找到要删除的节点
if (target === null) {
throw new Error(`[remove]not found key '${key}' in tree`);
}
}
// 1. 要删除的节点是没有子节点的叶子节点
if (target.left === null && target.right === null) {
return this.replaceNode(target, isLeftNode, parent, null);
}
// 2. 要删除的节点有一个 left 节点,没有 right 节点
if (target.right === null) {
return this.replaceNode(target, isLeftNode, parent, target.left);
}
// 3. 要删除的节点有一个 right 节点,没有 left 节点
if (target.left === null) {
return this.replaceNode(target, isLeftNode, parent, target.right);
}
// 4. 删除的节点既有 left 也有 right 节点
// 4.1 找到要删除节点的后继节点
let successorParent = target;
let successor = target!.right; // 后继节点(在右子树中寻找)
while (successor.left !== null) {
successorParent = successor;
successor = successor.left;
}
// 4.2 修改后继节点的 left 和 right 值
// 如果当前找到的后继不是 target.right 那么也就是说后继节点
// 就有自己的 right 节点, 那么就必须修改后继节点的 right 值
// 如图中要删除15的时候,那么后继节点就是 18, 18 有自己的
// right 节点, 19 这个节点不能直接丢弃
successor.left = target.left;
if (target.right !== successor) {
successorParent.left = successor.right;
successor.right = target.right;
}
// 4.3 替换
return this.replaceNode(target, isLeftNode, parent, successor);
}
}二叉搜索树的缺陷
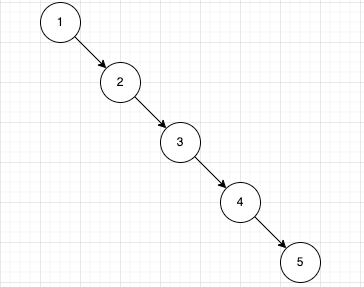
如果插入的 key 是递增的序列, 那么二叉树的深度非常大 也就是说一边特别多, 另外一边几乎没有, 两边极度不平衡 (所以: 二叉搜索树是一种非平衡树) 几乎就已经退化成了一个链表
typescript
const bst = new BinarySearchTree<number>();
'12345'.split('').forEach((item) => {
const num = Number(item);
bst.insert(num, num);
});
红黑树
TODO: 实现红黑树